Understanding Nova: Friendly Recursive Zero-Knowledge Arguments from Folding Schemes

Zero-knowledge arguments have revolutionized the field of cryptography, enabling secure and efficient verification of computations without revealing sensitive information. In this article, we delve into Nova, a cutting-edge approach to realize incrementally verifiable computation (IVC) - "friendly" Recursive zero-knowledge arguments. We will explore the fundamental concepts behind Nova, its IVC formation using what are called folding schemes, and evaluate its implementation and performance. Let's embark on this journey of understanding Nova's innovative contributions to the world of zero-knowledge arguments.

Nova itself is an incrementally verifiable computation that uses folding schemes in its construction. With a novel cryptographic approach that leverages zero-knowledge arguments to establish the correctness of step-by-step computations while preserving privacy. It offers an efficient and scalable solution by employing a non-interactive folding scheme, eliminating the need for resource-intensive techniques like succinct non-interactive arguments of knowledge (SNARKs). Nova stands out due to its simplicity, speed, and versatility, making it a promising alternative to existing methods.

At the core of Nova lies the concept of incrementally verifiable computation (IVC), which allows the prover to generate step-by-step proofs of correctness. Unlike traditional IVC methods, Nova's prover employs folding schemes to fold the previous step's computation into the current step, reducing computational overhead significantly. This folding scheme acts as the foundation for Nova's non-interactive approach, making it more efficient than its predecessors. Let's explore the key concepts behind Nova's formation and understand how it achieves its efficiency and scalability.

A folding scheme is a collaborative approach between a prover and a verifier to combine two instances of a problem into a single instance. The goal is to obtain a folded  instance-witness pair that is satisfies a relation if and only if the original instance-witness pair satisfies that relation. This technique aims to reduce the costs for the verifier, making it more efficient than verifying each original instance separately.

In Nova, folding schemes play a vital role by allowing the prover to fold the previous step's computation, represented as an instance of R1CS (Rank-1 Constraint System), into a running relaxed R1CS instance. This folding process occurs at each step of the computation, enabling the prover's proof to include both the current step's computation and the verifier's computation in the non-interactive folding scheme.

Nova's innovative approach relies on a non-interactive version of the folding scheme to achieve incrementally verifiable computation (IVC). IVC provides a means to prove the correctness of a step-by-step computation, where each step produces a proof that the verifier checks against the previous step's proof. This process continues until the final proof verifies the entire computation, without the verifier's work and proof size depending on the number of steps.

In Nova's IVC scheme, a specific type of computation known as relaxed R1CS is used for the incremental computation. At each step, the prover proves the correctness of that step's computation. Unlike traditional IVC approaches, which verify the proof for the previous step, Nova's prover folds the previous step's R1CS instance into the running relaxed R1CS instance. This integration allows for efficient and low-cost verification, reducing the computational overhead significantly.

A notable feature of Nova's IVC approach is the achievement of the smallest "verifier circuit" in the field. The verifier circuit in Nova is of constant size and primarily consists of two group scalar multiplications. This compact verifier circuit contributes to the efficiency of Nova's approach, making it faster than existing methods. Additionally, the prover's work at each step is dominated by two multi exponentiations of reasonable size, further enhancing Nova's speed and practicality.

By leveraging folding schemes and IVC from non-interactive folding schemes, Nova creates a powerful approach framework for IVC. This approach simplifies the verification process, reduces computational burdens, and improves overall efficiency compared to traditional methods. Nova's ability to fold computations and seamlessly integrate them into a running instance provides a novel and efficient solution for secure and scalable computation verification.

The implementation of Nova has been realized as a library in the Rust programming language. This versatile library supports various elliptic curve cycles and hash functions, providing flexibility in its usage. It accommodates the incremental computation step (F) through the integration of bellperson gadgets, enabling seamless integration into different systems.

To evaluate Nova's performance, extensive experiments were conducted, measuring key metrics such as prover time, verifier time, and proof sizes. The results showcased the remarkable efficiency of Nova. The recursion overhead, represented by the verifier circuit size, was found to be the smallest reported in the literature. In fact, Nova's recursion overhead is more than 10 times lower than SNARK-based IVC and over 100 times smaller than SNARK without a trusted setup.

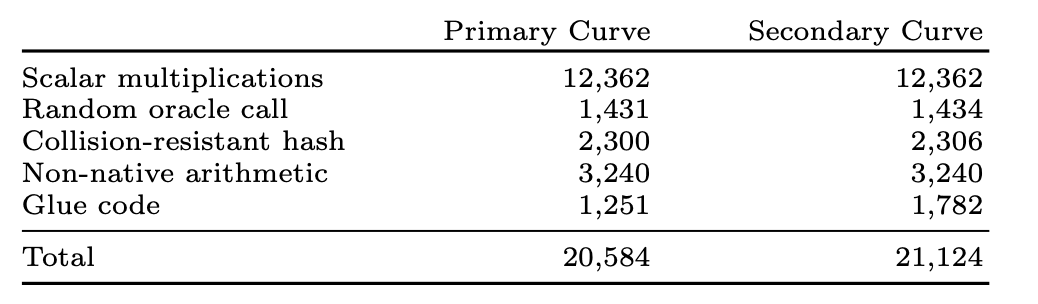
Furthermore, Nova's prover demonstrated impressive scalability, with the per-step cost of generating an IVC proof and compressing it scaling sub-linearly with the size of the computation. Compressed IVC proofs were notably compact, approximately 7,400 times shorter than their uncompressed counterparts. Verifying a compressed proof incurred only a modest increase in computational costs compared to verifying a considerably longer IVC proof.

Nova presents a remarkable advancement in the realm of friendly zero-knowledge arguments. Its innovative approach, based on non-interactive folding schemes and incrementally verifiable computation, allows for efficient and secure verification of computations. Nova's implementation and performance evaluations have demonstrated its efficiency, speed, and compactness. With its potential applications in various domains, Nova opens up new possibilities for privacy-preserving computation. As research in this field progresses, Nova's contributions are poised to shape the future of zero-knowledge arguments.

By understanding Nova and its underlying principles, we gain insight into the exciting realm of friendly zero-knowledge arguments and their transformative potential in enhancing privacy and security in computational systems.