Introduce PLONK: Revolutionizing ZK-SNARK Technology for Efficiency and Privacy

In the ever-evolving world of cryptography, privacy and security are paramount concerns. Zero-Knowledge Succinct Non-Interactive Arguments of Knowledge (ZK-SNARKs) have emerged as powerful cryptographic tools that allow individuals to prove the validity of statements without revealing sensitive information. Among various ZK-SNARKs, PLONK has taken center stage due to its remarkable efficiency and innovative approach. In this article, we explore the fascinating world of PLONK, delving into its inner workings, advantages, efficiency, and potential for future improvements.

PLONK, short for "Permutations over Lagrange-bases for Oecumenical Noninteractive arguments of Knowledge," is a general-purpose zero-knowledge proof scheme devised by Ariel Gabizon, Zac Williamson, and Oana Ciobotaru. Zero-knowledge proofs allow one party (the prover) to demonstrate knowledge of specific information to another party (the verifier) without revealing the actual details. This makes ZK-SNARKs highly valuable in applications that require secure data sharing and privacy-preserving transactions.

Building upon the advancements of protocols like SONIC and Marlin, PLONK introduces several key improvements to enhance the usability and efficiency of zero-knowledge proofs.

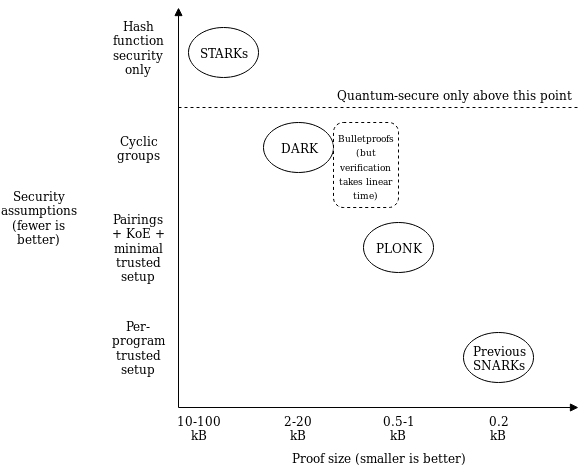
Source: Understanding PLONK - Vitalik Buterin's website

Universal and Updateable Trusted Setup: Like many other zero-knowledge proof schemes, PLONK still requires a trusted setup procedure. In a trusted setup, a set of initial parameters is generated, and the security of the scheme depends on keeping these parameters secret. However, PLONK's trusted setup is universal and updateable. This means that instead of needing a separate trusted setup for each program to be proven, there is one single trusted setup that can be used with any program (up to a certain maximum size defined during setup). Additionally, the trusted setup can involve multiple parties, and it remains secure as long as at least one of the participants is honest. This multi-party procedure is sequential, allowing participants to be added over time, which increases the safety of the setup in practice.

Standardized Component - Polynomial Commitment: PLONK relies on a single standardized component called a "polynomial commitment." Polynomial commitments are cryptographic tools that enable efficient verification of polynomial equations. PLONK uses "Kate commitments," which are based on trusted setups and elliptic curve pairings. However, the scheme is flexible, allowing alternative schemes like FRI or DARK to be used instead. This means that different trade-offs between proof size and security assumptions can be achieved by swapping out the polynomial commitment scheme. The ability to choose different schemes caters to various use cases and developer preferences.

PLONK converts a problem represented by a computer program into a set of polynomial equations using essential concepts: gate constraints and copy constraints.

1. Gate Constraints: These equations relate the values of wires attached to the same gate in the circuit. Logic gates for addition and multiplication form the circuit representation in PLONK. Each gate takes input wires and produces an output wire based on specific operations. For example, a multiplication gate with inputs A and B and output C would have a gate constraint: C = A * B. These constraints accurately represent the circuit's operations, allowing the verifier to confirm correctness without knowing the prover's inputs.

2. Copy Constraints: Copy constraints ensure the equality of different wires within the circuit. They preserve the flow of data by enforcing that the output of one gate matches the input of another. For instance, if two wires A and B must have the same value, the copy constraint would be: A = B.

By employing gate and copy constraints, PLONK achieves a compact and efficient representation of the problem, making it scalable and practical for various applications requiring zero-knowledge proofs.

To understand more about formulas and math. We recommend you to read this article from Vitalik.

1. Enhanced Prover Efficiency: PLONK significantly reduces the prover's computational burden, requiring only five polynomial commitments and two opening proofs. This efficiency sets it apart from other ZK-SNARKs like Sonic, making it ideal for applications demanding efficient computation. 2. Compact SRS Size: PLONK boasts a smaller Structured Reference String (SRS) size, crucial for generating ZK-SNARK proofs. Its compact SRS size aligns with the circuit's number of gates, substantially reducing required storage compared to other ZK-SNARKs. This enhances efficiency and scalability in real-world use cases.

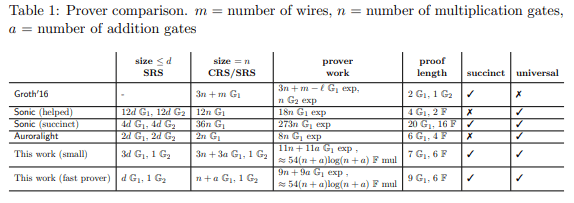
Table Source: PlonK: Permutations over Lagrange-bases for Oecumenical Noninteractive arguments of Knowledge

Benchmarking experiments demonstrate PLONK's remarkable performance. Proofs constructed for circuits containing over a million gates take under 23 seconds on consumer-grade hardware. Comparisons to FFT and elliptic curve scalar multiplications highlight PLONK's optimized execution of cryptographic operations, reinforcing its efficiency.

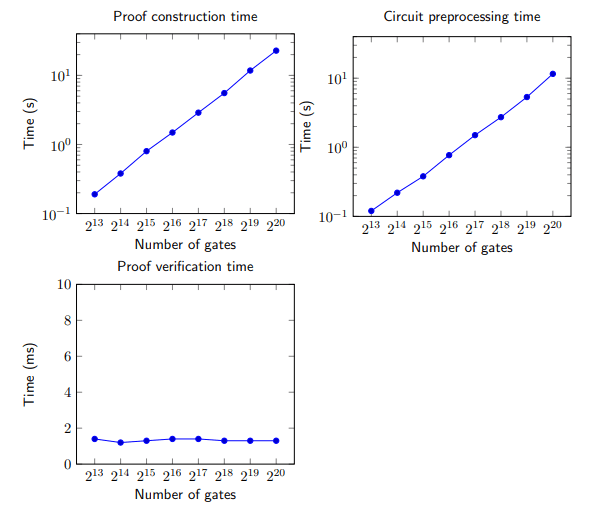
Table Source: PlonK: Permutations over Lagrange-bases for Oecumenical Noninteractive arguments of Knowledge

In a comparison to FFT (Fast Fourier Transform) and elliptic curve scalar multiplications, PLONK demonstrates its prowess. The FFT costs associated with PLONK are on par with elliptic curve scalar multiplications, emphasizing the efficiency of PLONK's computational operations. This demonstrates the optimized execution of essential cryptographic operations within PLONK.

1. Integration of Sparse Bi-variate Evaluation: PLONK is considering incorporating the technique of sparse bi-variate evaluation from other ZK-SNARKs like Fractal and Marlin. This integration aims to achieve efficient verification of linear constraints, further streamlining validation and enhancing overall efficiency. 2. Enhanced Efficiency and Flexibility: PLONK explores the potential to combine permutation checking with sparse bi-variate evaluation, capitalizing on their strengths. Such integration could improve efficiency and flexibility, enabling PLONK to handle a broader range of gate types effectively. 3. Exploration of Optimization Opportunities: Continual research seeks to optimize PLONK's performance across various metrics, including prover and verifier run times, proof length, and SRS size. This dedication ensures PLONK remains at the forefront of efficient cryptographic protocols. 4. Adapting to Emerging Use Cases: PLONK strives to adapt to emerging technologies and applications, ensuring its compatibility and effectiveness in addressing future cryptographic challenges.

PLONK heralds a new era of efficiency in ZK-SNARKs. With its unique permutation argument and simplified representation of Lagrange polynomials, PLONK offers exceptional benefits, including enhanced prover efficiency and reduced SRS size. The benchmarking experiments have validated PLONK's efficiency, making it a top choice for real-world applications. As ongoing research drives potential improvements, PLONK continues to lead as a groundbreaking ZK-SNARK construction, empowering individuals and organizations with secure, privacy-preserving cryptographic solutions.