Advancing Succinct Non-Interactive Proofs with HyperPlonk

Succinct Non-Interactive Proof (SNARK) systems have revolutionized the field of secure computation by enabling efficient verification of complex computations without revealing sensitive information about the inputs. Among these, Plonk has garnered attention for its short proofs and quick verification. However, Plonk's reliance on FFT computations has posed challenges, especially for large circuits. In response to this, the innovative HyperPlonk protocol emerged as an adaptation of Plonk, offering significant advancements in efficiency and flexibility.

About Plonk:

Plonk, based on Polynomial-IOP, is a widely-used SNARK system that can handle various arithmetic circuits, including custom gates. Its proofs are concise, around 400 bytes, and quickly verifiable. However, Plonk's complexity arises from the need for FFT computations, leading to potential bottlenecks for larger circuits. This limitation prompted the exploration of alternative proof systems with different trade-offs to suit specific scenarios.

About HyperPlonk:

HyperPlonk is a novel extension of Plonk designed to function on the boolean hypercube, a structure of binary values (0 and 1) organized in a specific manner. A key advantage of HyperPlonk is its elimination of the computationally-intensive FFT step during proof generation, resulting in a much faster prover. Moreover, HyperPlonk supports higher-degree custom gates without compromising the prover's efficiency. The protocol achieves this through multilinear polynomial commitments over the boolean hypercube, which necessitated modifications to accommodate this unique mathematical structure.

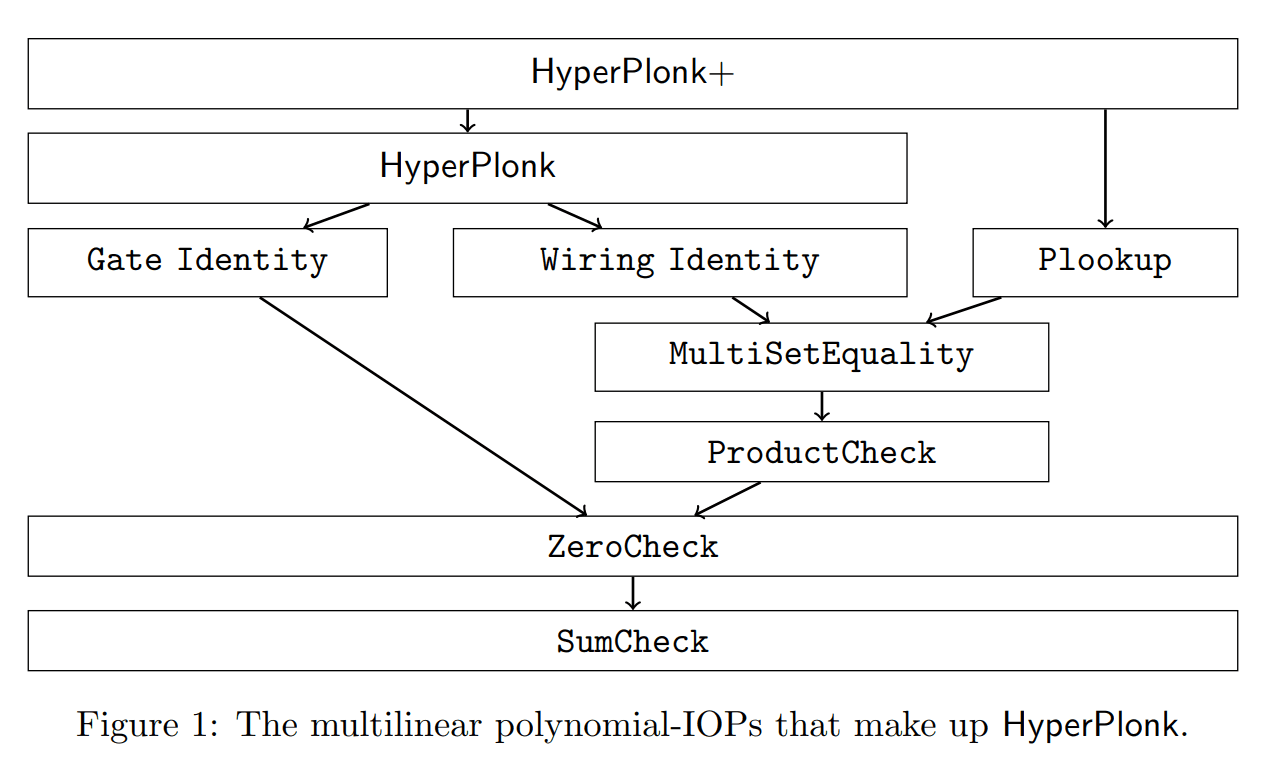
HyperPlonk introduces several crucial distinctions from its predecessor. It represents computations using multilinear polynomials over the boolean hypercube, providing more efficient manipulation of computation. Moreover, HyperPlonk uses gate and wiring identities to ensure proper evaluation and correct circuit wiring, respectively. The protocol also leverages the ZeroCheck and SumCheck IOPs to verify the committed polynomials' correctness without relying on FFT computations, thus enhancing the prover's speed.

HyperPlonk introduces a powerful and efficient approach to verifying mathematical computations by utilizing multilinear polynomial commitments over the boolean hypercube. The protocol's core functionalities are rooted in two crucial components: the Gate Identity and the Wiring Identity.

The Gate Identity plays a fundamental role in verifying that all gates within the arithmetic circuit are accurately evaluated. To achieve this, the prover is required to demonstrate that the polynomial it committed to satisfies specific constraints for each type of gate, be it addition, multiplication, or custom.

This critical validation process is facilitated through a technique known as ZeroCheck. The ZeroCheck allows the prover to showcase that the committed polynomial consistently evaluates to zero for all possible inputs represented by binary values within the boolean hypercube. By demonstrating this property, the prover ensures that every gate in the circuit functions as intended, culminating in the correct output.

source: HyperPlonk: Plonk with Linear-Time Prover and High-Degree Custom Gates

The Wiring Identity serves as a crucial assurance that the connections between gates in the circuit, known as wiring, are precisely configured. The prover's responsibility lies in demonstrating that the committed polynomial adheres to specific constraints that accurately represent the wiring of the circuit.

To achieve this verification, HyperPlonk employs a set equality protocol, which reduces the wiring problem to a ProductCheck. This ProductCheck is then further reduced to a ZeroCheck, leveraging insights from earlier works, namely Bayer and Groth and Quarks.

Through this sequence of reductions, the prover effectively proves that the committed polynomial meets the correct wiring constraints, ultimately safeguarding the integrity of the entire computation.

In summary, the prover in HyperPlonk employs two distinct methods to demonstrate the correctness of the computation:

1. Proving the Gate Identity: By utilizing ZeroCheck, the prover showcases that the committed polynomial satisfies the specific constraints associated with each type of gate within the circuit, ensuring proper gate evaluations.

2. Proving the Wiring Identity: Leveraging set equality protocols and a sequence of reductions, the prover ensures that the committed polynomial satisfies the accurate wiring constraints, guaranteeing the correct interconnections between gates.

HyperPlonk's ingenious combination of multilinear polynomial commitments and these verification mechanisms enables it to achieve unparalleled efficiency and security in verifying complex computations over the boolean hypercube. By eliminating the need for computationally-intensive FFT computations and supporting higher-degree custom gates, HyperPlonk marks a significant leap forward in the realm of succinct non-interactive proof systems. Its ability to provide quick and reliable verification without compromising privacy makes it a promising contender for a wide range of real-world applications.

HyperPlonk effectively employs the ZeroCheck and SumCheck protocols to verify the committed polynomials' correctness, a critical step for ensuring the integrity of the proof. These protocols obviate the need for FFT computations, significantly reducing the proof generation time and enhancing overall protocol efficiency.

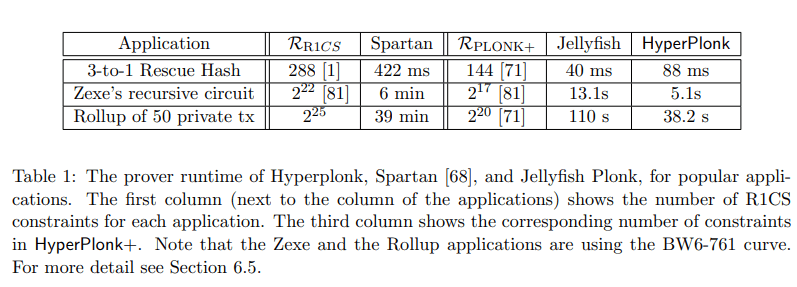
In response to the prover's challenge of opening multiple multilinear polynomials, HyperPlonk introduces the innovative "batch-opening" protocol. This protocol allows simultaneous opening of multiple polynomials, reducing proof generation time, proof size, and verification time. The efficiency of this protocol is measured in terms of field operations, with substantial improvements achieved in comparison to prior methods.

HyperPlonk further enhances efficiency by introducing improvements to the multilinear commitment scheme. The Orion+ multilinear commitment scheme reduces proof size while maintaining the prover's time efficiency, representing nearly a 1000x improvement in proof size. Additionally, a generic transformation technique converts a univariate polynomial commitment scheme into a more efficient multilinear commitment scheme, achieving quantum resistance and quasilinear time complexity.

source: HyperPlonk: Plonk with Linear-Time Prover and High-Degree Custom Gates

HyperPlonk addresses the issue of soundness error in the existing permutation PIOP when used with µ-variate polynomials. By proposing an alternative permutation PIOP with a significantly smaller soundness error, HyperPlonk becomes more suitable for use with small fields in polynomial-based protocols. Although this improvement slightly affects the prover's efficiency, the tradeoff ensures improved soundness properties, crucial for maintaining security and correctness.

HyperPlonk stands as a remarkable advancement in the field of succinct non-interactive proof systems. By mitigating the bottlenecks associated with FFT computations, embracing the boolean hypercube, and introducing innovative protocols, HyperPlonk offers superior efficiency and flexibility over its predecessor, Plonk. As cryptographic protocols continue to evolve, HyperPlonk sets a compelling standard for secure and efficient verifiable computation, paving the way for future advancements in the field.